Gravity
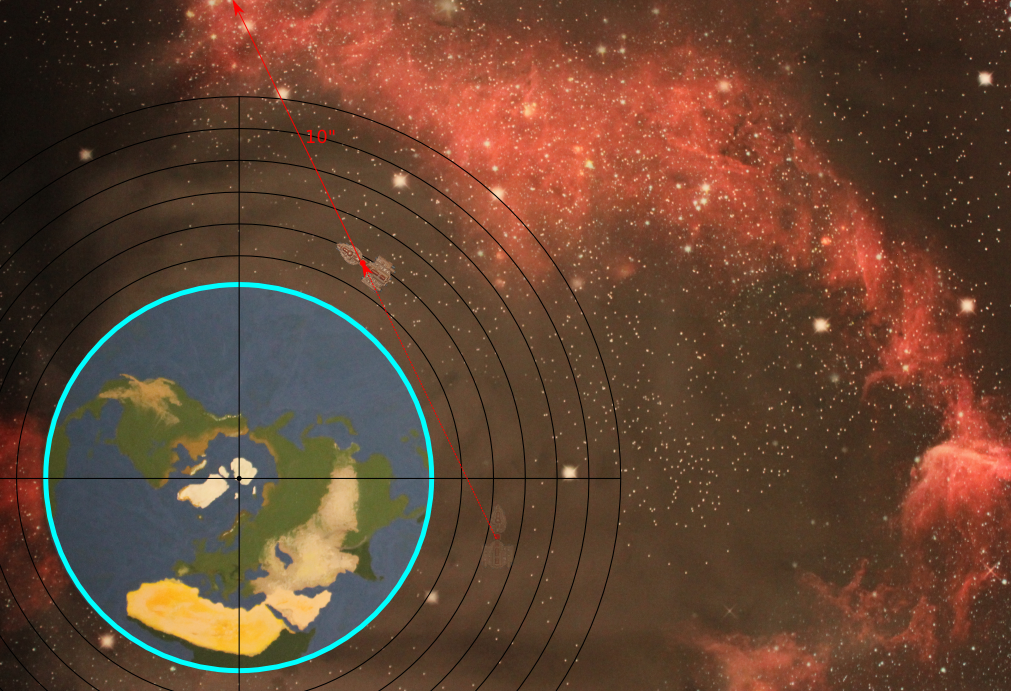
The following rules model gravity from the bottom up, so require a few extra measurements when a ship is manoeuvring close to a planet. Each planet will have a number of gravity zones above its surface (during the game all measurements are taken from the surface of the planet, not it's centre) which dictate the strength of the gravitational field at that point. The radius of these zones increases in a geometric progression - 2“, 4”, 8“, 16” and beyond.
The following are values for some common planets and moons.
| Acceleration at distance from surface | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Planet | Diameter | Gravity | 2“ | 4” | 8“ | 16” | 32“ | 64” | 128“ | 256” |
| Earth | 13“ (12,700km) | 1g | 6T | 4T | 2T | 1T | – | – | – | – |
| The Moon | 3” (3,475 km) | 0.15g | 1T | – | – | – | – | – | – | – |
| Mars | 7“ (6,787 km) | 0.3g | 2T | 2T | – | – | – | – | – | – |
According to physics, gravity will cause a ship to accelerate towards the planet. For this reason, gravitational strength is treated as thrust, as if the ship were thrusting towards the planet. A ship within 2” of the surface of the Earth will have 6 thrust towards the surface.
If you want to work out values for your own worlds, there there's a simple(ish) formulae for doing so, which will be given at the end of this page.
Gravitational Movement
The rules here assume that you are using the vector movement system, and work best if you have a counter for each ship showing its vector. When a ship is moved, you apply the ships normal manoeuvring to that counter, but before you actually move the ship you need to account for gravity.
- Work out which zone the ship is currently in, and look up the gravitational acceleration.
- Work out the direction from the centre of the ship to the centre of the planet.
- Apply the gravitational acceleration to the movement counter in the same direction as in step 2.
- Move the ship as normal.
Movement Example
Step One: Work out gravitational force
As an example, consider the NAC ship Aggressor that is performing a flyby of the Earth. At the start of its movement it is within 3“ of the Earth, moving at a velocity of 8” mostly parallel to its surface.
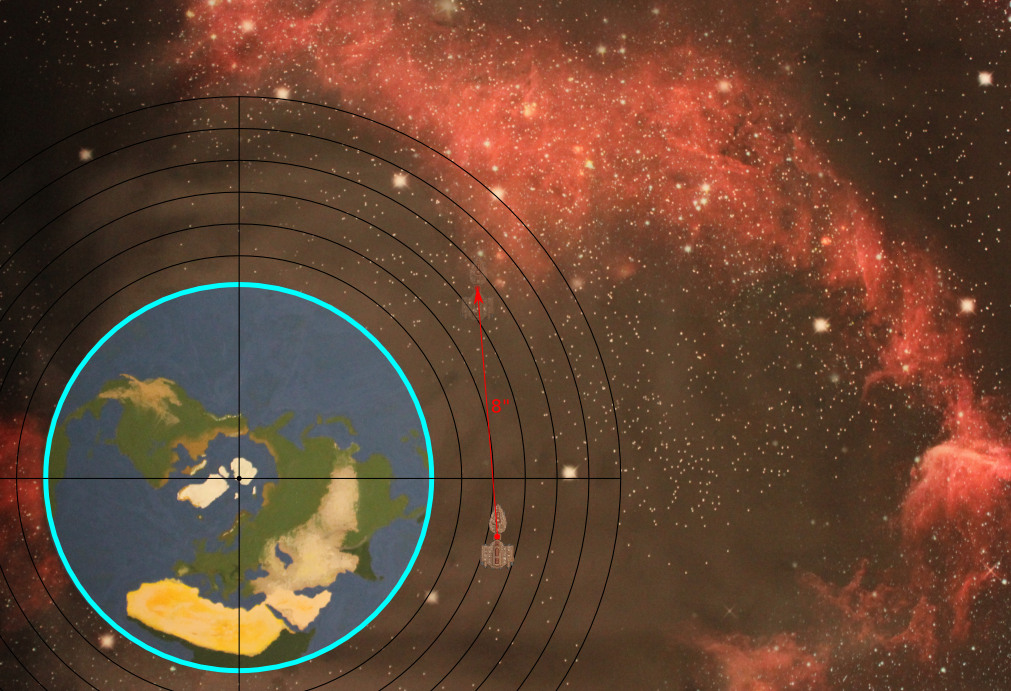
Since the Aggressor is in the 2“-4” zone, the gravitational force on it applies a thrust of 4. At no point during this example will the Aggressor use its own drives - all movement changes will be entirely due to the Earth.
Step Two: Work out direction of force
We next work out which direction the force of gravity applies. This is always in the direction from the ship's starting location towards the centre of the planet.
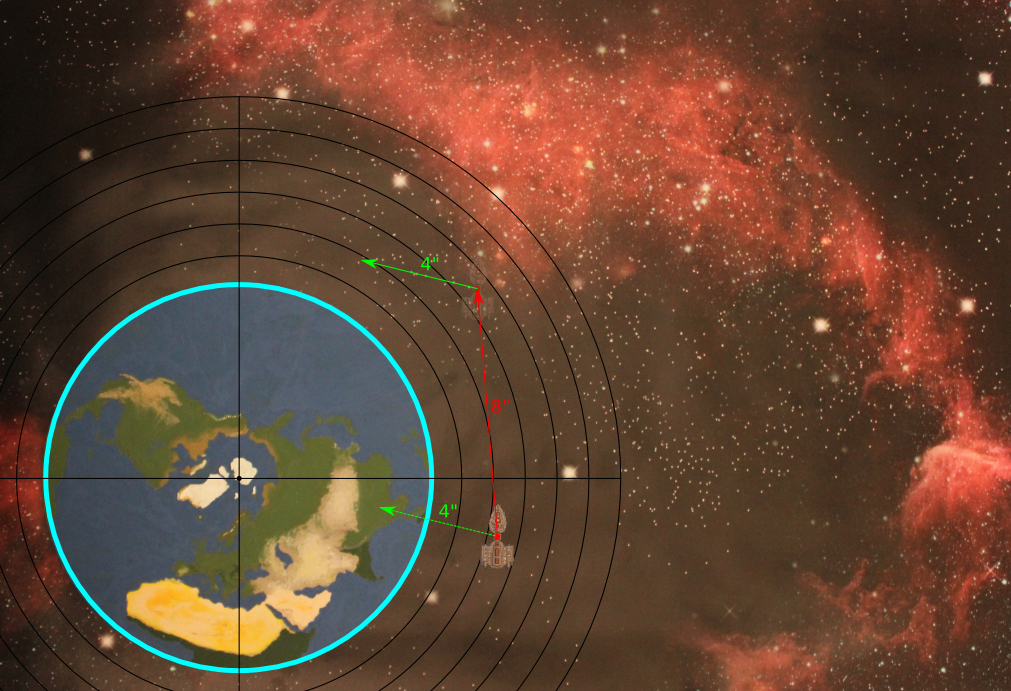
We find the vector from the Aggressor to the centre of the Earth. This is the direction that the ship is being dragged towards the planet - the direction is always taken from the start of movement. Since the gravitational thrust is 4“, we apply a vector of 4” to the destination point in the same direction.
Step Three: Determine final vector
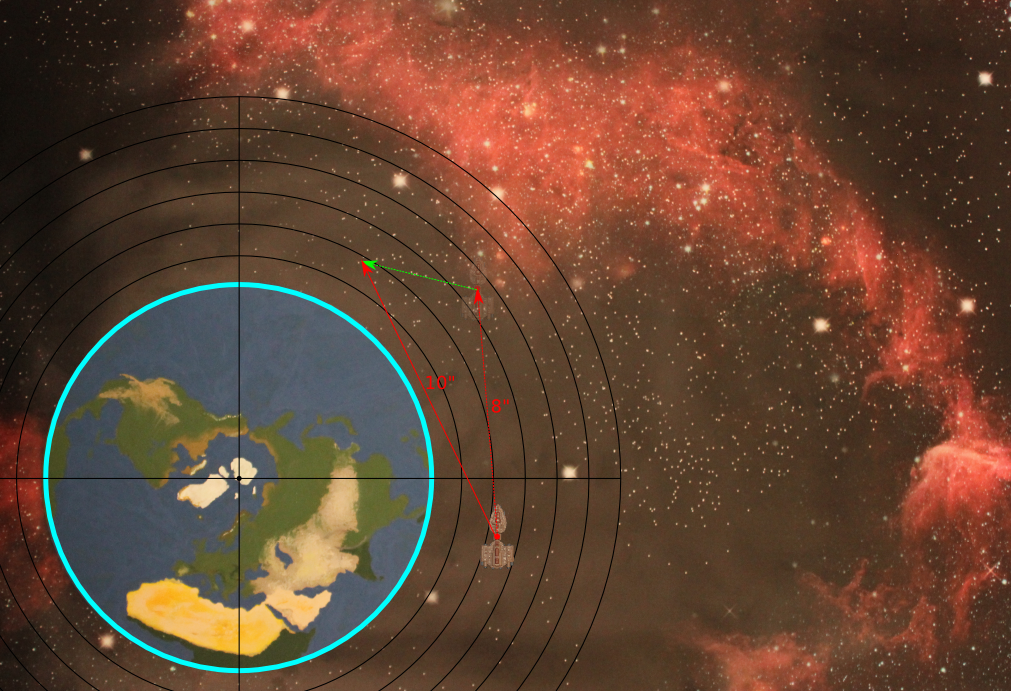
Step Four: Move the ship